Drawings to sort Click and drag into the bins below
,(1,4,3,2)(5,6),(1,7)(2,3)(4,6,5).png "(1,7,2,4,6)_(1,4,3,2)(5,6)_(1,7)(2,3)(4,6,5)")
B
,(1,2,3,4)(5,6),(1,3,2)(4,5)(6,7).png "(1,5,7,6,4)_(1,2,3,4)(5,6)_(1,3,2)(4,5)(6,7)")
B
,(1,2,3,4)(5,6),(1,2)(3,5,4)(6,7).png "(1,5,7,6,3)_(1,2,3,4)(5,6)_(1,2)(3,5,4)(6,7)")
A
,(1,2,3,4)(5,6),(1,7)(2,3)(4,5,6).png "(1,6,4,2,7)_(1,2,3,4)(5,6)_(1,7)(2,3)(4,5,6)")
B
The four pictures below are dessins d'enfants (or children's drawings). They each describe a Belyi map from a surface to the sphere. Three of the maps are related by symmetries of the algebraic numbers that define them, while one map stands alone. Can you spot the odd one out?
In this case, one map stands alone because we can describe it with rational numbers, which have no symmetries besides the identity. To describe the other three maps, we also need a root of the polynomial \(x^3 - x^2 + 2x - 38\). These three maps, and the numbers that describe them, are related by the symmetries that exchange the roots of the polynomial.
A Belyi map is a special kind of map from a surface to the sphere.
In 1979, G. V. Belyi proved that an algebraic curve over \(\mathbb{C}\) can be defined over \(\overline{\mathbb{Q}}\) if and only if it admits a Belyi map. In this case, the Belyi map can also be defined over \(\overline{\mathbb{Q}}\).
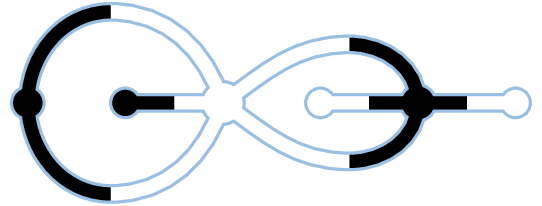
A dessin d'enfant is a special kind of ribbon graph. A ribbon graph is a finite set of dots connected by ribbons, which glue to their edges.
A dessin d'enfant is an orientable ribbon graph where each ribbon has a black end and a white end. Black ends glue to black dots, and white ends glue to white dots. We require dessins to be connected.
A ribbon graph is completed when it's embedded in a surface so that its complement is a set of disks. Any ribbon graph can be completed, by gluing disks along the loops formed by the sides of the ribbons. Since a dessin is a kind of ribbon graph, dessins can be completed too.
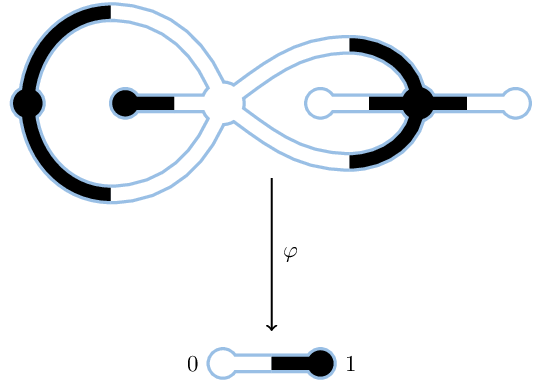
Dessins let us describe Belyi maps using pictures instead of formulas.
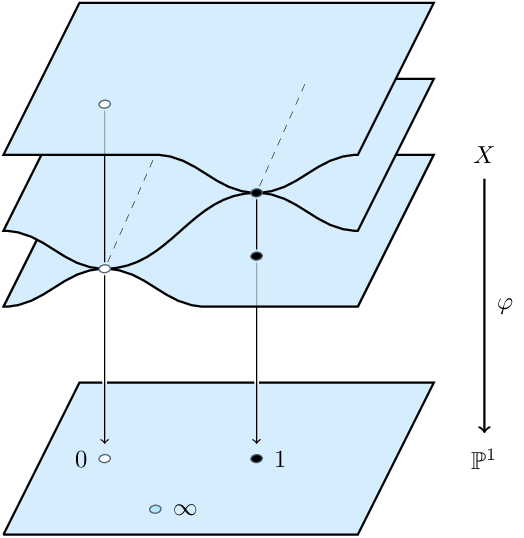
In 1984, Alexander Grothendieck pointed out that a Belyi map \(X \to \widehat{\mathbb{C}}\) gives a completed dessin d'enfant on \(X\) by pulling a prototype dessin back from \(\widehat{\mathbb{C}}\). He proved that the Belyi map is fully described by its dessin, and that every completed dessin on \(X\) describes a Belyi map.
The prototype dessin on \(\widehat{\mathbb{C}}\) has a white dot at \(0\) and a black dot at \(1\), connected by a ribbon along the interval \([0, 1]\).
If there's a Belyi map \(\varphi \colon X \to \mathbb{P}^1\), both \(X\) and \(\varphi\) can be defined by equations with coefficients in \(\overline{\mathbb{Q}}\). This lets the absolute Galois group \(\operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})\) act on the set of Belyi maps: an element of \(\operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})\) acts on \(\varphi\) by acting on its coefficients.
The bijection between Belyi maps and dessins induces an action of \(\operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})\) on the set of dessins. Grothendieck wondered if one could understand the action of \(\operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})\) on Belyi maps through its induced action on dessins. In particular, can one tell if two dessins are related by the Galois action just by studying their combinatorial or topological features? That would give a very concrete way of understanding the important and mysterious group \(\operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})\)!
In this game, we give you a collection of dessins, and you try to sort them into Galois orbits—that is, to put them in the same box if they're related by the Galois action. Can you find some distinguishing features that tell you two dessins belong together? This is no small feat, so don't be discouraged if you get stumped!